Here is a typical three-dimensional mixed shape problem that requires knowledge of a couple of basic rules.

A pyramid with a square base and altitude h has four equal edges e that meet at the vertex V. If e is equal to b, what is the value of h in terms of b? (Figure not to scale.)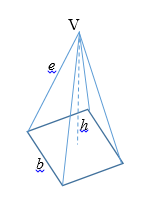

SOLUTION:

Notice that we can create a right triangle with an edge by using one-half of the base’s diagonal. First we figure the bottom leg of that triangle by looking at the square base:

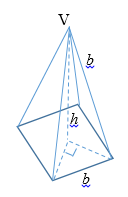
Using the 45-90 rule (which is used almost every time a square is present in the problem), we see the bottom leg of this right triangle is equal to:      b/√2

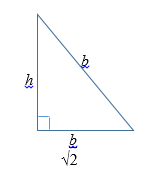
Solving for h using Pythagorean:

h²         =          b²    -     (b/√2)²

h          =          √(b²/2)

h          =            b/√2

 

 

---