Path of a bullet and a Pair of Equations
In my social and political science classes, I give at least one lecture during the semester on the Scientific Method. We discuss our human tendency to doubt scientific evidence or theories if they challenge our beliefs, and how our “common sense” can at times mislead us. The following is one of many examples:
Suppose you are standing outside, facing a flat open field, as far as the eye can see. You have a gun in one hand, pointed straight and level toward the field. (We have to assume all safety precautions have been taken and no one is in range.) In your other hand, you’re holding a bullet at the same level as the gun. At the precise instant you fire the gun, you also drop the bullet. I then propose to the class: “Common sense tells me the bullet I drop will hit the ground sooner than the bullet I fired way out into the field, right…?” Some students nod their head in agreement, and generally the class shrugs that they're OK with that conclusion. However, this is where our common sense is at odds with the math and science.
Physics tells us the bullets will hit the ground at the same time, assuming there is no wind resistance (which can be significant) or elevation differences. Taking this further, how can we explain the trajectory of that bullet fired from the gun? This is an example of parametric equations, where we compare the horizontal and vertical components of this projectile motion.
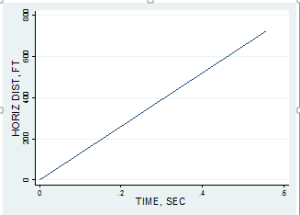
Assume the gun is 5’ off the ground and the muzzle velocity is 1300 feet per second. After the instant of firing, the only force acting on the bullet is gravity, applying only to the vertical component. The horizontal velocity, v, of the bullet is independent of this vertical pull of gravity, and therefore remains constant, assuming no wind resistance. (This law of inertia can be difficult to grasp, that the bullet would otherwise continue at a constant speed infinitely.) The relationship between horizontal distance, dx, and time, t, is represented through the general equation, dx = vt, one that pops up on the standardized tests occasionally. The graph is a straight line with a y-intercept of 0, and a slope of v:
dx = 1300t
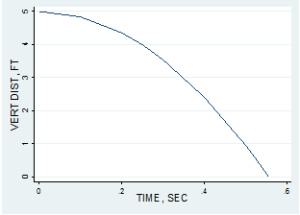
The vertical distance, dy, or the height of the bullet from ground, can be represented through the quadratic equation dy = - ½ at2 + h, where a is the acceleration due to gravity (32.2 ft/sec2), and h is the initial height of the bullet from the ground. This is a reconfiguration of the standard physics equation (d = vot + ½ at2), where in our case the acceleration is negative, so we can visualize this graph as an inverted parabola:
dy = -16.1t2 + 5
Thus we have the horizontal and vertical distance equations as a function of time:
dx = 1300t
dy = -16.1t2 + 5
In this case, setting dy equal to 5 will give us the time it takes the dropped bullet to hit the ground, which is 0.557 seconds. Plugging this into the first equation gives a horizontal distance of 724 feet, or about two and a half football fields (not accounting for the decelerating force of wind resistance). However, combining the two equations (substituting for t) will give us the graph of the trajectory, dy versus dx:
dy = -16.1(dx/1300)2 + 5
dy = - (1/105,000) (dx)2 + 5
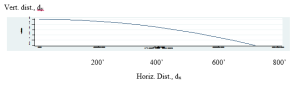
A parabola is represented by the quadratic equation f(x) = ax2 + bx + c, where the “a” coefficient (not to be confused with acceleration) tells us something important toward visualizing the graph. Particularly, if the “a” coefficient is negative, the parabola is inverted, and as the absolute value of "a" becomes a smaller fraction, the parabola will get wider. This is what we see here with the bullet’s trajectory. Clearly the dy to dx graph is not to scale, otherwise it would look much like a flat line. We are only getting a small tip of the inverted parabola in this case.
As we have stressed in the math instruction, it is useful to visualize what such formulas and equations are describing, to better understand what they mean and how to work with them.
RKL for Maximatician.com
