Circumference of the earth from a 13′ pole
How might we figure the circumference of the earth with just a 4 meter pole? First it helps to know that the sun will be directly overhead Town A at 12:00 noon on June 22, the summer solstice, when the sun's zenith is at its furthest point from the equator. At that moment, you will plan to be in Town B, 800 kilometers away. We can assume the sun's rays are parallel to the one coming down directly overhead Town A.
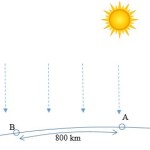
Holding the pole upright at Town B (at a right angle to the earth's surface), you measure a shadow that is ½ meter long. Zooming in on the pole in Town B, we can see the shadow formed:
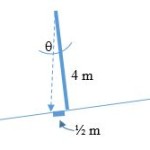
The angle theta formed at the top, between the pole and the sun’s ray can be found with trigonometry:
tan theta = opposite over adjacent = 0.5/4 = 1/8 = 0.125
The angle theta is 7.1°
Extending the ray at Town A and the pole in Town B to the center of the earth, we see – since the sun’s rays are parallel - the measure of the earth's central angle that corresponds (or, alternate interior angles) with the arc length of 800 km is also 7.1°:
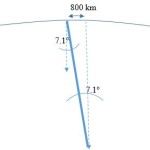
Now we can use the arc length-central angle ratio to calculate the earth's circumference, C.
7.1/360 = 800/C
C = 40,560 km
By the way, this is what Eratosthenes did around 235 B.C. to estimate the earth’s circumference, where Towns A and B were Syene (now known as Aswan) and Alexandria, Egypt, respectively. The actual circumference ranges from 40,008 to 40,075 (due to the bulge at the equator), so Eratosthenes was only about 1.2% higher. Not too bad.
What is even more fascinating is that Eratosthenes - a contemporary of Archimedes - was aware that our planet was a sphere, something that was not (re)confirmed in Europe until 15 centuries later!
Sources:
Dunham, William. 1990. Journey Through Genius: The Great Theorems of Mathematics. New York: Penguin Books.
Hewitt, Paul G. 2010. Conceptual Physics, 11th Edition. Boston: Addison-Wesley.
